Tree in Data Structure

In this article Tree in Data Structure we give the information about A tree is a non-linear type of data structure. A tree is a finite set of nodes with one specially designated node called the root and the remaining nodes are divided into disjoint sets.

Tree in Data Structure:-

Stack, queue and linked list data structures are linear in nature. There are many applications in real life situations where non-linear data structures are used. Graphs and trees are non-linear data structures. In non-linear data structure, one-to-many relationship exists. It is used to represent hierarchical relationship existing among several data items. The directory structure of computer system is a example of nonlinear data structure.

Definition:

A tree is a non-linear type of data structure. A tree is a finite set of nodes with one specially designated node called the root and the remaining nodes are divided into disjoint sets. Where each of those sets is a tree.

tree

Example:

In the above figure A, B, C, D, E, F, G, H are the nodes of the tree and data item A is the root of the tree. the remaining notes are partitioned into two sets (trees) with B and C as their respective roots.

Tree Terminology

Root

The topmost node i.e., the first node in the hierarchical arrangement in a tree is called as a root node. In the above figure, A is the root node.

Node

A node in a tree represents each data item of the tree. In the above figure A, B, C, D, E, F, G and H are the nodes.

Degree of a node

The number of sub trees of a node is called as a degree of a node.

In the above figure,

The degree of A is 2
Also The degree of C is 1
And The degree of B is 2

Degree of a tree

It is the maximum degree of nodes in a given tree. The degree of the above tree is two.

Leaf node or terminal node

A node with degree zero is called as a leaf node. In the above example D, E, G and H are leaf notes. It also called as terminal node.

Non-terminal node

Any node (except the root node) whose degree is not zero is called non-terminal node. There are three non-terminal nodes in above example.

Parent node

A node with other nodes connected to it is called as parent node. In other words, nodes other than leaf nodes are parent nodes.

In above figure, A, B, C and F are parent nodes.

Siblings

The children of the same parents are called as siblings. In above example,

B and c are siblings of A
D and E are siblings of B

Level

The position of the node in the hierarchy is called as the level of the node. The root node is considered to be at level 0. In above example levels are shown.

Edge

The line connecting two nodes is called as the edge.

Path

The sequence of consecutive edges, which join the source and destination nodes, is called as path.

Depth

The maximum level of any node in a tree is called depth of the tree. It is also called as the height of the tree.

Forest

A forest is a set of disjoint trees. A forest can be obtained by removing the root node of any tree.

Binary Trees

A binary tree is a tree in which each node has at most two child nodes. The two child nodes of a parent node are called as left sub tree and right sub tree.

In a binary tree the maximum degree of any node is at most two. It means, there may be a zero degree node also called as empty tree or a one degree node and two degree node.

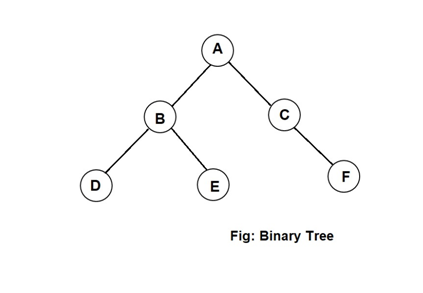
binary tree

In the above binary tree. A is the root of the tree. The left sub tree consists of the tree with root B. In addition, the right sub tree consists of the tree with root C. Further B has its left sub tree with root D and right sub tree with root E. Similarly, C has empty left sub tree and its right sub tree with root F.

Types of binary tree

Strictly binary tree
Complete binary tree
Skewed binary tree
Binary search tree

Strictly binary tree

A strictly binary tree is a binary tree where all non-terminal nodes have two branches.

Strictly binary tree

Complete binary tree

A complete binary tree is a strictly binary tree with all its terminal nodes at the same level.

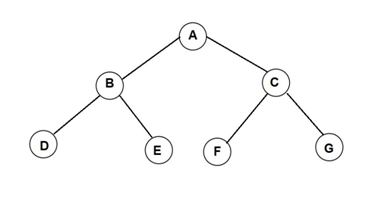
Complete binary tree

Skewed binary tree

The branches of this tree have either only left branches or only right branches. Accordingly, the tree is called left skewed or right skewed tree.

Skewed binary tree

Binary Search tree

A binary search tree in which the nodes are arranged according to their values. The left node has a value less than its parents and right node has a value greater than the parent node. That is all nodes in the left sub tree have values less than the root and those in the right sub tree have values greater than the root.