Representation of binary tree

In this article Representation of binary tree we give the information about There are two ways by which binary tree can be represent array representation of a binary tree and Linked list representation of a binary tree.

Representation of binary tree

There are two ways by which binary tree can be represent

1. Array representation of a binary tree
2. Linked list representation of a binary tree

1. Array representation of a binary tree

It is requires three arrays. One array ‘data’ stores the information fields of the trees. The other two arrays ‘leftarr’ and ‘rightarr’ represents the left child and right child of the nodes.

Following figure represents the array representation of tree shown above.

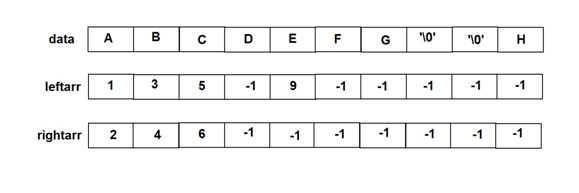
The array leftarr and rightarr contains the index of the array data where the information is present. If the node does not have any left or right child then element in leftarr and rightarr contains the value -1. The root is always stored at 0^th position of an data array. ‘\0’ represents an empty child.

Consider the example that we want to find the left and right child of the node C. the index value of C in data array is 2. So find the values present at 2 in leftarr and rightarr. The value present at index 2 in leftarr is 5, which is the index position of node F in the data array. So the left child of C node is F. The value present at index 2 in rightarr is 6, which is the index position of node G in the data array. So the right child of C node is G.

2. Linked list representation of a binary tree

Binary tree can represented using linked list. The basic component to represent binary tree is a node. The node consist of three fields as follows

• Info
• Left child
• Right child

The info field stores the data. The left child is a pointer which stores the address of its left node and the right child contains the address of the right node.

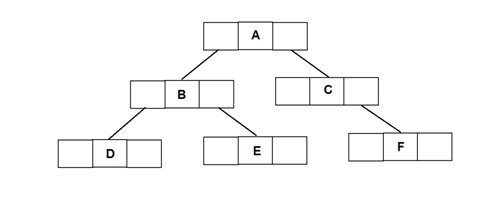
Following figure represents the linked list representation of tree shown above

The data structure in C is given below:

struct node

{

int info;

struct node *left;

struct node *right;

};

typedef struct node *NODE;

Operations on binary tree:

     The various operations performed on binary tree are as follows:

1. Create binary tree
2. Tree traversal (Displaying the tree)
3. Insertion of node
4. Deletion of node
5. Searching a node
6. Computing the height of the tree
7. Copying binary tree
8. Counting the total nodes
9. Counting total leaf nodes
10. Comparing two binary trees

Some More: 

POP- Introduction to Programming Using ‘C’

DS – Data structure Using C

OOP – Object Oriented Programming 

Java Programming

DBMS – Database Management System

RDBMS – Relational Database Management System

Join Now: Data Warehousing and Data Mining