Strassen Matrix Multiplication: Divide & Conquer Algorithm for Fast

Strassen Matrix Multiplication uses Divide & Conquer to multiply large matrices efficiently. Learn the algorithm, steps, time complexity, advantages, and applications.

Strassen Matrix Multiplication

(Strassen’s Matrix Multiplication Method)

Introduction

Strassen’s Matrix Multiplication Algorithm is an advanced and efficient Divide and Conquer–based algorithm used to multiply two square matrices faster than the traditional method.

In the traditional matrix multiplication algorithm, the time complexity is O(n³).
Strassen reduced this complexity to:

O(n^log₂⁷)≈O(n^2.81)

which makes it significantly faster for large matrices.

Need for Strassen’s Algorithm

When the size of matrices becomes large, the traditional matrix multiplication method becomes very time-consuming.

Strassen’s algorithm:

Reduces the number of multiplications
Is more efficient for large matrices
Improves overall performance in matrix computations

Divide and Conquer Approach

Strassen’s algorithm is based on the Divide and Conquer technique.

Divide Step

Let A and B be two square matrices of size n × n.
Each matrix is divided into four equal sub-matrices:

Matrix A:

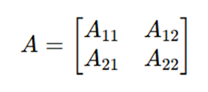
Matrix B:

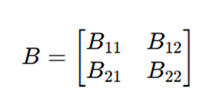
Traditional Method vs Strassen Method

Traditional Matrix Multiplication

Requires 8 multiplications
Requires 4 additions
Time Complexity: O(n³)

Strassen’s Method

Requires only 7 multiplications
Uses some extra additions and subtractions
Time Complexity: O(n^{\log_2 7}) ≈ O(n^{2.81})

Strassen’s Seven Multiplications

Strassen proposed the following seven intermediate products:

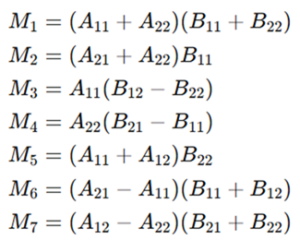
Final Result Matrix (Combine Step)

Using the above intermediate values, the result matrix C is obtained as:

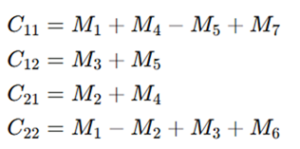
Algorithm Steps

If the matrix size is 1 × 1, multiply directly (Base Case)
Divide each matrix into four sub-matrices
Perform 7 recursive multiplications
Combine the sub-results to form the final result matrix

Time Complexity Analysis

The recurrence relation for Strassen’s algorithm is:

T(n)=7T(n/2)+O(n2)

Using Master’s Theorem, we get:

T(n)=O(nlog27)≈O(n2.81)

This is asymptotically better than the traditional O(n³) algorithm.

Advantages

Reduces the number of multiplications
Faster for large matrices
Efficient use of the Divide and Conquer technique
Useful in high-performance and scientific computing

Disadvantages

Not efficient for small matrices
Requires extra additions and more memory
Implementation is complex
May suffer from numerical stability issues

Applications

Scientific computing
Computer graphics
Image processing
Machine learning and Artificial Intelligence
High-performance computing systems

Conclusion

Strassen’s Matrix Multiplication Algorithm is a powerful Divide and Conquer–based technique that significantly speeds up matrix multiplication.
Although it is not suitable for small matrices, it outperforms the traditional method for large matrices and is widely used in advanced computing applications.

See More: